Estimating Time Of Arrival

           One of the most common calculations you make when cruising, whether it’s a sail on the Bay or island hopping in Greece, is figuring when you’re going to get where you’re going. It’s easy enough to estimate time of arrival when you are “fetching” your destination, which is sailing jargon for sailing directly there rather than tacking. Distance divided by speed equals time. But suppose you want to figure out how long it takes to sail to San Francisco from Richmond. With the prevailing summer wind, it’s going to be a beat and let’s say your boat does 6 knots through the water, but not in a direct line because you have to tack. The “ETE” or estimated time enroute, and “VMG” or velocity made good aren’t so straightforward, and these are what you need to know to figure “ETA,” or estimated time of arrival. You can figure a rough estimate, though, without knowing trigonometry or having a whole cabal of nerds running arcane computer programs for Larry Ellison.
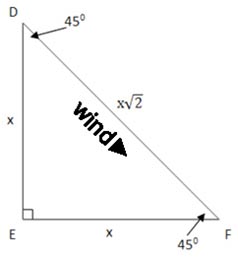
                What you’ve got when your destination is directly upwind is, theoretically, an isosceles right triangle (iso=equal, skelos=leg) where the hypotenuse represents the distance to your destination and the legs represent your tacks. So x + x is the distance you’ll have to sail to get from F to D via point E:

            
                Remembering that geometry class in high school, a squared + b squared = c squared, but since the legs are the same, the hypotenuse is equal to either side times the square root of two. (In this theoretical treatment it doesn’t matter whether it’s ten tacks or one.) So if you divide the hypotenuse, which is in this case the distance from the end of Potrero Reach (F) to the City (D), about 5.5 nautical miles, by the square root of two (≈1.41), you’ll have the length of one tack, and then multiply by two for the two tacks, you will have the distance you need to sail to get there. This turns out to be a little less than 8 nm. Let’s assume a boat speed of 6 knots with a steady breeze. If you divide that distance by your six knots of speed, you’ll have your time enroute or ETE, about 1.3 hours. Divide the distance from F to D by the ETE, 5.5/1.3, and you’ll have your velocity made good or VMG, a little more than 4 knots. And add the ETE to the present time, and you’ll know if you’ll be arriving in time to meet Betty and Sam.  
                Because that calculation is neglecting leeway, however, the distance is actually a little more than that so your ETE is longer and your VMG is less. So forget all that square root stuff. It turns out that just multiplying the distance from F to D by 1.5 is going to give a close enough estimate of the actual distance you’ll have to sail, assuming the destination is dead to windward, for us regular old sailors. Correspondingly, your VMG is 2/3 of your boat speed through the water. If it isn’t dead to windward, sail the long leg first, and the multiplier will be less than 1.5, but never less than 1. It’s not so hard. So put those high school trig and geometry books back on the shelf next to your vinyl Spice Girl albums.
                But wait. We also have to figure current, as the above assumes slack water. This can get a bit cumbersome but let’s see if we can, again, find a shortcut. Have a look at the current charts at the back of your tide book. Turn to the max ebb chart on p. 59. You’ll see 1.4 knots helping you along, then a little over 2 knots of current to the right. This is on an average day at maximum current. To find what the figure is on a strong day, go to the chart on p. 50 and you’ll see the multiplier is 1.5. This means that at max ebb on a strong day, you’ll get 1.4 x 1.5, or a little over 2 knots of help halfway there, and then let’s say 2.4 x 1.5 or about 3.5 knots of being set to the right, which also helps. Averaging those, you’ll have a bit less than three knots in your favor for the whole trip. When we add this to the six knots your boat does over the water, we get a speed over the water of nearly nine knots on a day with a strong ebb. The distance sailed is the same 8 miles, so now the trip will take just less than an hour at max ebb on a strong day. [There is some oversimplification going on here, but…let’s just forget about that.]
                On a flood where the current is adverse, consult the chart on p. 53, and again adjusting by the chart on p. 50, we’ll multiply by 1.5 for a strong day. We get 1.5 knots of adverse current and then a little less than 2 setting us to the left, opposite of where we want. (The flood difference is smaller than the ebb difference because on average the ebb is stronger than the flood. A subject for another day.) Averaging the 2 with the 1.5, we can subtract 1.7 knots from our boat speed, bringing it to about 4.3 knots. The distance through the water is the same 8 miles, so it will take a little less than 2 hours to get there. Again, this is max flood on a strong day.
                The end result is we get a range of ETE from just under one hour with a strong ebb, which yields a VMG of about 6 knots; one hour, 20 minutes at slack for a VMG of just over 4 knots; and a little under 2 hours against a strong flood for a VMG of about 2.8 knots. Try this for any destination on the Bay. If any of you decide to actually do this, please report your results back for all of us to benefit. There’s nothing like empirical validation.
                OK, I admit, that was a bit complicated. But you only have to figure this out once, based on the speed of your boat, and you’ll know at a glance how to estimate your ETE to the city given the state of wind and current. All of this assumes constant wind and consistent boat handling, so your figures may vary. Not that you really care, because if you’re sailing, no matter how long it takes to get to your destination, you’ve already arrived.